The need for AC
There are still a few specialist applications where low-voltage AC power is 'a must' = essentially, any application where an AC 'synchronous motor' is in use or where power needs to be transferred over long distances
CCTV (and PoE)
CCTV cameras are usually powerd by a 24v AC feed. The current demand per camera is typically about 1A (or half that if no anti-dew 'heater' is incorporated in the camera housing). Many CCTV camera's will accept DC, however some insist on AC (perhaps because they incorporate an AC fan) and, needless to say, you will find that 24 VAC transformers cost 'an arm and a leg' !
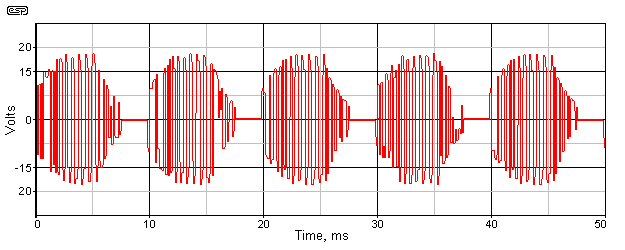
Available at much lower cost are 'electronic transformers'. These essentially consist of a mains 'chopper' circuit and small high frequency transformer. The output AC is (typically) 20-50kHz with an amplitude (voltage) that varies over the 50Hz (or 60Hz) mains input cycle.
Above:- Typical output from a "12v Electronic Transformer" (from http://sound.whsites.net/lamps/elect-trans.html ) Whilst the 'chopped' AC high frequency varying output is fine for incandescent bulbs (lighting) use, sending it down a 1km cable (even twisted pair) will likely result in massive RFI ! Worse, from the user point of view, is that the CCTV camera likely incorporates rectification diodes not designed for high frequency use (so they will typically overheat) or, worse, (especially older ones) may come equipped with an input transformer designed for 50Hz (not 50kHz :-) )
Power over Ethernet (PoE)
When it comes to Power over Ethernet, this uses DC voltages for distances up to about 100m. However over long distances (say, 1km) the voltage drop will be excessive. One solution is to switch to AC, although, again, sending 20-50kHz up 1km of cable is not going to make you very popular with your neighbours :-)
Note that using an AC feed is the only (simple) way to get dual voltages at the PoE device end (a 24vac feed can be half-wave rectified to give +/- 12vdc = such dual voltage will be required to drive AC motors with a 'common ground')
Cheap AC motors
There are any number of small AC motors available on eBay that are driven with 50/60 Hz AC. Since these are 'dual frequency', we can guarantee they will operate at 55Hz +/- 5Hz with a good bet that they will work from 45-65Hz (i.e. 55 +/- 10)
The massive advantage of such motors are that you can 'guarantee' the speed will be whatever the AC drive is set to (unlike a DC servo motor where the speed varies with voltage and load, so can't be used to get a specific rotational speed without some sort of speed sensor and feed-back circuit) The massive disadvantage is that all 'low end' AC motors start up rotating in a random direction (i.e. they are 'CW/CCW' types)
Dual winding AC motors (with a 'start widing' and (often) external 'start' capacitor) will start up in a specific direction, as will any 3 winding (3 phase) motor, however these are hard to find at the 'low end' (low cost, factional horse power) rating
For a start-winding motor, search ebay for "Synchronous AC Electric Gear Motor 220V 5 RPM Reversible" (about £8).
An alternative to using an AC motor would be to use a DC Stepper Motor (such as the 24BYJ4 or 28BYJ-48) which has the additional advantage of holding it's position when 'stopped'. Even with a drive chip (ULN2003 is common) these can be had for less then £2. Both direct drive and geared versions can be found on eBay (the 28BYJ-48 is a 5v stepper with 16:1 gear box - other ratios commonly available are 36:1, 60:1, 100:1)
AC generation
The 'electronic transformer' does 'point the way', however it's high-frequency output is 'full wave' (with a 50Hz 'amplitude' variation), so can't just be 'filtered' to give 50Hz. Instead the driver output must deliver a real '+ve half cycle' followed by a real '-ve half cycle'
Whilst 'analogue' driver (using a DAC and power amplifier) could deliver the sine-wave voltage variation, losses (and heat) is minimised by using a (high-frequency) Pulse Width Modulation (PWM) approach. The (high frequency) PWM can deliver a sine-wave varying 'average' voltage, but must switch from a +ve voltage drive to a -ve voltage drive every 20mS (for 50Hz = 40mS full cycle) To avoid the need for dual voltage supply, the driver circuits will typically 'reverse the wires' at the output each half cycle (so, for the first half cycle, the driver outputs +v,0 and on the second half 0,+v) == this, of course, only 'works' so long as there is NO OTHER GROUND (0v) REFERENCE at the 'destination' i.e. it works for motor windings with no 'common ground' (0v reference) To save on cost, some 3 phase motors have only 4 wires i.e. 3 drive wires and a common ground. Such motors can't be driven using the 'reverse the drive wires' trick and require true dual voltage drive (only those with 3 seperate windings (i.e. 6 wires) can be driven by reversing the voltage)
The actual drive can be achieved using an off-the-shelf L298N (dual full H bridge) costing £1.50 (or less) from eBay (China, post free). The L298N board even includes a small +5v regulator, so, when fed with (up to) +12v motor drive voltage (so +/-12v = 24vac), the drive board will also power a 5v PIC. The L298N board supports a 25kHz PWM drive frequency, so using a basic 4MHz (1 MIPS) PIC as the 'speed controller' should be a simple task.
The L298N is a dual full H bridge. Both 'H' sets connect to a single motor supply (V+) voltage input. Each H has it's own 'Gnd' output (so you can fit a current 'sense' resistor between that and Gnd), 2 control inputs (one for each side of the H), a common 'enable' (if enable is Lo, then the entire H is 'off' i.e. no connection to either common motor voltage or Gnd is made)). Each side of the H has it's own motor drive output, which is connected to either V+ or Gnd, as determined by the control input (input Hi, drive Hi, input Lo, drive Lo). The L298N thus has 4 drive outputs, which means it can drive 4 separate uni-directional servo motors (or a stepper motor with 4 phases). If the outputs are 'paired up' (to form a full 'H' drive), then it can drive 2 reversible servo motors = and this is what allows it to generate an AC waveform.
PWM from a 1MIPS PIC
Whilst 1 MIPS sounds like a lot of instructions, when we are aiming at 25kHz PWM that's only 40 instructions per cycle ! If we drop the PWM frequency to 20kHz, then we have 50 instructions 'per cycle' and (assuming we can achieve control to within 1 instruction step) that means we have 1/50 = 2% control over the output 'mark-space' (or 'on=off') ratio.
A 20kHz PWM also sounds like we have plenty of PWM cycles per 55Hz sine-wave cycle, however it's actually only 20k/55 = 363.3r. In fact, 181.81 of these define the +ve side of the sine wave and 181.81 the -ve side.
The 'fractional' PWN cycles can be 'used up' in the 'dead band' between the half cycles, however that makes the PIC code more complicated. So what happens if we stick to using complete PWM cycles for each AC half-cycle ? Well 182 PWM cycles per half wave will generate a 54.945 Hz AC drive = and a single PWM cycle change to 183 per half gets us 54.645 Hz (and 180 gets us 55.55r Hz), so we have almost 1/2 Hz control (ie. better than 1% for a 55 Hz 'nominal' drive).
Generating (half) sine-waves
I found Microchip application note AN1523 Sine Wave Generator Using Numerically Controlled Oscillator, however this is virtually useless. The first 10 pages relate to square wave generation (and the use of filters to get the sine wave), but does give some hints about the use of the counter/timer and an 'incrementing accumulator' approach. Page 11 gives a few more hints about using a Look-up-table but then the rest of the AN goes off into a lot of floating point calculation nonsense. Of much more use was PWM Sine Wave Generation for AVR Arduino - whilst the code is 'aimed' at the Arduino Atmega368P it focuses on PWM sine wave generation from page 1. Finally, I found the older Mictochip AN65 = whilst the R-2R DAC ladder shown on Pg2 is plainly nonsense (in the real world you will be lucky if you can get 4 or 5 'more or less' linear binary stages, no way can you get the 8 shown !) it gives actual code for a DTMF keyer (from pg 6)
To generate a (half) sine wave, the PWM mark-space is changed gradually from 'off' (0%) to 'on' (100%) for the first quarter wave - and then 'reversed' (on to off) for the second quarter wave. The 'ramp down' is the inverse of the 'ramp up', so to generate a half wave, all we need is an approach that will generate the correct mark-space ration for the first 1/4 cycle, which can then be run 'backwards' for the next 1/4.
Since the second half cycle is just a repeat of the first with the output voltages reversed, once we have the first 1/4 cycle it's 'job done'
The obvious approach is to use some sort of look-up-table, HOWEVER we have to cope with the fact that the output frequency needs to vary = so, whilst a table of 91 entries would give us 182 (x2) steps for 55Hz (actually 54.945 Hz) we would then need another table for each other frequency supported. Worse, whilst 182 divides nicely to give us 91 per 1/4 cycle, the 1/2Hz PWM 'next step' counts (181, 183) would result in 'half cycles' ! One method would be to hold a higher resolution 'position to mark-space' LUT - say 255 values - and generate a 'step count' (that adds to the position) for the specific frequency you need (which t would then be used to select a sub-set of values from the table). On the other hand, each PWM cycle is only 50 clks. So there can only be 50 possible mark-space values. Rather than hold a 255 location LUT that translates 'sine-wave position' into mark-space (and which by definition, will contain many identical values), a 50 location LUT could store the '% position' in the sine-wave at which each of the mark-space ratios takes effect. The final approach is to note that the mark-space values will be 'stepped' up (or down) by some small value between 0 and perhaps 3 or 4 i.e. the step can be 'encoded' in 2 or 3 'bits'.
Before going any further, we need to select a PIC to generate the waveform. The 'lowest possibe cost' choice is the PIC12F675 = these can be had for as little as 20p each (eBay China, 10pcs). These devices have 1k program space, 64 registers, 128 bytes of eeprom, 6 i/o lines, an 8bit timer (with pre-scaler), a 10bit A/D and 1 comparator. The internal OSC is 4MHz (1 MIPS), external goes to 20MHz (for 5v operation)
For minimum cost, the internal OSC will be used (it has been factory pre-calibrated to within 1%, although it's a good idea to read the cal. value before using the k150 programmer on it). It should be easy enough to fit the sine-wave generator into 1k program space, even if 255 locations have to be 'reserved' for a LUT. In theory the eeprom could be used for the LUT, however access is via a 'pointer register' and 'data latch', plus requires you toggle a 'read operation bit' before you can retrieve a value from a data latch = so the 'overhead' on reading the eeprom is +4 CLK's (on top of any address calc etc) Eeprom write speeds are much, much slower, typically 10mS per byte (and that's assuming you don't have to erase the target location first)
50 step 1/4 sine-wave LUT
Since we have only 50 possible mark-space ratios, a 50 entry LUT will define the '% position' at which each of the 50 mark-space values takes effect (actually, since 'off' (0) is position 0 and 'on' is position 255, we actually only need 48 locations)
Since we need to maintain accuracy, the 'position' will need to be held as a 16 bit value = the top byte of which corresponds to the LUT entry. Operation is as follows :- To start generation, PWM is 'off' and the running total step count is set to 0. The 16bit 'step' increment is then pre-calculated from the frequency required 'fr' as follows :- There will be 1,000,000/4*fr CPU CLK's per 1/4 cycle (so, for fr=50 Hz, that's 5,000) = call this 'Fclks'. If 1/4 cycle = count 0xFF (or to be more exact 0xFFFF), then each micro-step is 0xFFFF/Fclks .. however we are only going to iuncrement the step 'count' after each PWM ccyle .. is the 'PWM step' is 50*0xFFFF/Fclks. Substituting we have :- 'PWM step' = 50*0xFFFF/ (1,000,000/4*fr), = 4*fr*50*0xFFFF/1,000,000, = fr*0xFFFF / 5,000 = fr*13.107 (0x00 0D 1B) If fr is held as a single byte, to an accuracy of 1/4Hz, then fr max is 0xFF = 255/4 = 63.75Hz. Max. step is at max. fr and performing a 'raw' 1/4Hz count * 0x000D1B at 1/4 count 0xFF gives us 0x0D0DE5 (after which we divide by 4 and round up to 16 bits to get 63.75Hz step of 0x0343 (50Hz gives us a step of 0x028F). As usual, mark-space 'off' (0x00) and 'on' (0xFF) will be treated as 'special case' (when off or on is reached, then we have reached the end of a 1/4 wave and have to prepare for the next) THe PWM is software generated. The transition will be somewhere in the 50 Clk cycle - and the calculations for the next PWN cycle will need to be done in the 'long half' of the cycle (since the 'short half' could be as short as 1 clk :-) ). This means that the '50/50' hs to be treated as s 'special case' (i.e. switch from one half to the other). Finally, we 'step forwards and backwards' each 1/4 cycle (i.e. add the steps for the leading 1/4, subtract the step for the trailing 1/4). Any 'remainders' are carried forward into the 'next' 1/4 cycle (so, on average' we get higher than PWN cycle precision)
This reduces the calculations to an initial '1/4Hz * 13.107' (fr byte * 0x0x00 0D 1B, divided by 4) to get the 16bit step increment (actually, the 16bit increment will have to be recalculated every time the fr is changed)
Sine-wave generation consists of successive 16bit addition/subtraction (once per PWM cycle) with an 8bit look-up and compare (to discover if the position (running step total) has crossed into the next PWM mark-space value). The add (or subtract), look-up and compare all has to be done within the current PWM cycle.