What are the basic measurements ?
OK, so we have a basic design - we are going with a standard (full size) 'Arc Drive' BarnDoor that will be driven at 1 rpm. Now we need to do some calculations of arm size etc.
The Drive Nut will be turned at (exactly) 1 rpm (this is key to both Manual use and later motorisation) - and this must compensate for the rotation of the Earth against the stars.
Calculating the (anti)rotation speed
From first principles ... (or skip direct to the calculation of the M12 rod to hinge distance below) ..
We have to counteract the Earths rotation - so how fast is the Earth 'spinning' then ?
The intuitive answer is 'once a day' i.e. once in 24 Hours. Well, yes, but "one day" means "from when the sun is overhead to when it is (exactly) overhead again". This is known as the Solar Day = and it is indeed 24 Hrs.
What we need to known is the actual rate of rotation 'against the stars' (this is known as the "Sidereal Day") - see below or visit Wikipedia/Sidereal Day.
Earth's real rate of rotation against the stars (the Sidereal Day)
If the Earth was not rotating (= spinning) at all, then it would take the whole year for us to see the Sun to go from exactly overhead to exactly overhead again.
If the Earth was spinning at exactly 'once a year' AND it was spinning in the same direction as it travels around the Sun, then we would end up with 2 (solar) days per year.
If the Earth was spinning against the direction of rotation around the Sun (actually, it does), then a 1 rev per year spin would exactly cancel out the 'yearly' day and it would be 'mid-day' all the time (and the same side of the Earth - the 'day' side - would always face the sun).
It was once thought that Mercury behaved like this - but a real example is the Moon. As the Moon rotates around the Earth it spins in the 'opposite' direction at exactly the opposite rate (i.e. 1 revolution per Lunar Month). So the Moon ends up with one (same) side toward the Earth all the time. We thus see the same side of the Moon all the time (leading to the popular misconception that the moon does not rotate at all :-) ). NB. this is not an accident - see Wikipedia "tidal locking">.
OK, back to the Earth.
In one year we have 365 1/4 (solar) days [365 days per year plus 1 extra day every 'leap year' = 365 1/4 on average approx. ]. It's actually 365.2422 solar days per year, which takes 365.2422 * 24 hours (i.e. 8,766 hrs or 525,948.768 mins).
Just like the Moon, the Earth is actually spinning in the 'opposite' direction - so the real rate of spin (actual number of revolutions in a year) is 1 extra, i.e. during each year Earth actually rotates 366 1/4 times.
Thus Earths rate of spin (the 'sidereal day' = rate against the stars) is one year (52,5960 mins) divided by 366.25 = 1436.068 mins (23 Hrs 56 mins 4 seconds). This is actually quite noticeable - if you look at the position of some known star at midnight every day you will see it gradually 'drifting'. The star will reach exactly the same position 4 minutes earlier each day - so if you check where it is each midnight you will find it has 'moved on a bit' each day.
Back down to Earth again ...
We want to turn our Drive Nut at exactly once per minute (1 rpm) in order to counter-act the Earth's rotation against the stars.
The Earth rotates once in 1436.068 mins. So if we want to turn the nut at 1 rpm, then 1436.068 turns of the Nut must counter-act 1 turn (360 degrees) of the Earth.
The distance from the Hinge to the centre of the screw rod is the Radius of the circle travelled by the arm and the distance travelled is the circumference of the circle = 2 * Pi * R.
Each turn of the Nut will move the arm a distance equal to the Screw Pitch. 1436 * Screw Pitch = one complete circle.
So we have 2 * Pi * R = 1436 * Screw Pitch.
Screw rod pitch
The above equation has two 'unknowns' - the Radius R (which we can choose when we construct the arms) and the Screw Pitch. Since we have little choice but to use a commercially available screw bolt, the only real choice is the Radius.
Solving for the Radius (distance from the Hinge to the centre of the screw bolt), we have R = 1436 * Screw Pitch / 2 * Pi [or approx 228.5556 times the Screw Pitch]
Bolt sizes ?
The table below shows the 'radius' required for various bolt sizes.
| Bolt size | screw pitch (mm) | Radius (full) | Radius (half) |
|---|---|---|---|
| M8 | 1.25 | 285.7 | 142.8 |
| M10 | 1.5 | 342.8 | 171.4 |
| M12 | 1.75 | 399.97 | 200 ** |
** a M12 bolt is rather too thick to be bent to a 200mm radius :-)
M12 rod to hinge distance
The standard ('coarse') thread M12 rod bolt has a screw pitch of 1.75mm. Of course, when we bend the bolt, the pitch is going to be smaller on the inside & larger on the outside of the bolt, however the Nut pitch won't change (and nor will the length of the bolt), so the pitch will still be 1.75 mm 'on average' - and one turn of the Nut will move it along the bolt by 1.75mm.
Thus R = 1.75 * 228.5556 = 399.97 mm (i.e. 15.75 inches or approx 400mm) = and this is the Hinge to bolt distance. This applies to a full sized 1rpm 'BarnDoor' = for a "half sized" system (half rpm), this distance is halved to 200mm.
How much rod bolt thread do we need ?
With most digital camera's we will only need (relatively) short exposures. At 1 rpm, a 10 minute exposure = 10 turns of the nut, will move the nut along the bolt (and hence the top arm along the arc) by 17.5 mm (i.e. 10 times the bolt pitch).
Of course we what to avoid 'resetting' the system every 10 minutes whist observing - so I chose a more usable bolt length of 105mm (which will gives one hours observation before it needs to be reset).
Note - it is vital that some sort of 'limit stops' are installed to prevent 'over-run' = it is all too easy to set up an exposure sequence of 10 x 10 min shots :-)
What's the base (tip over) angle ?
The BarnDoor has to rotate about the Earth's axis. So the base arm has to be 'tipped up', so that the Hinge can be pointed skyward and (in the northern hemisphere) lined up with the 'North Star' (of which more later).
Again, from basic principles, the North Pole is at 90 deg N, so the angle from the ground to the barn-door Hinge would have to be 90 degrees i.e. we would need to point the hinge straight up in order to align it with the North Star - as a result the bottom arm would have to be tipped up on is front edge and the BarnDoor really would look like a barn door :-)
Plainly the angle we need from the ground to the base arm hinge is equal to the Latitude at the observing location. In my case, this is approx. the same as London (U.K.), which is 51 deg. 32 min N or approx 51.5 degrees (actually, I live at 51 deg. 31 min).
How to measure the base 'tip over' angle ?
Well, if the base is 100mm wide, then a 'riser' drawn straight up a distance of (Tan(51.5)*100 =) 125.7mm allows us to complete a 'triangle' to get the required angle - see diagram below.
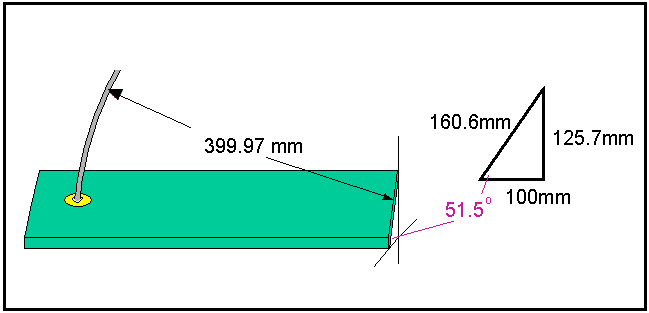
The other distance to make up the triangle would be 160.6mm.
It is should be quite easy to cut triangles of wood to dimensions 100 x 128 x 160mm, however absolute accuracy is not too vital, since we will need to have some means of adjusting the angle to cope with an uneven ground surface anyway.
The diagram also shows the other critical dimension, from the center of the screw rod to the center of the henge, is 399.97mm (OK, lets call that 400mm :-) )
Note that the 51.5 degree 'tip over' angle is between the bottom arm and 'flat' ground - since any random patch of ground is highly unlikely to be 'flat', the whole unit will need to sit on a base with adjustable 'feet' (see later)
So much for the basic design - click Next>> (left) for the actual construction ...